@datagrok/diff-grok v1.0.6
Diff Grok
A lightweight TypeScript library for solving initial value problem (IVP) for ordinary differential equations (ODEs) using numerical methods. This library focuses on solving stiff equations.
Features
- Solving both stiff and non-stiff equations
- Fast computations
- A set of Rosenbrock–Wanner-type methods:
- Scripting:
- declarative specification of models
- auto-generated JavaScript code
- Integration with the Datagrok platform
- Zero dependencies
Installation
npm i @datagrok/diff-grokSolving
General
To find numerical solution of a problem:
$$\frac{dy}{dt} = f(t, y)$$ $$y(t_{0}) = y_0$$
on the segment $t_0, t_1$ with the step $h$:
Import
ODEsand a desired numerical method:Specify
ODEsobject that defines a problem:name- name of a modelarg- independent variable specification. This is in object with fields:name- name of the argument, $t$start- initial value of the argument, $t_0$finish- final value of the argument, $t_1$step- solution grid step, $h$
initial- initial values, $y_0$func- right-hand side of the system, $f(t, y)$. This is a function(t: number, y: Float64Array, output: Float64Array) => void:t- value of independent variable $t$y- values of $y$output- output values of $f(t, y)$
tolerance- numerical tolerancesolutionColNames- names of solutions, i.e. names of the vector $y$ elements
Call numerical method. It returns
Float64Array-arrays with values of an argument and approximate solutions.
Diff Grok is designed to provide fast computations. Check performance for the details.
Example
Consider the following problem:
$$\begin{cases} \frac{dx}{dt} = x + y - t \ \frac{dy}{dt} = x y + t \ x(0) = 1 \ y(0) = -1 \end{cases}$$
To solve it on the segment $0, 2$ with the step $0.01$ using the MRT method with the tolerance $10^{-7}$, we start with imports:
import {ODEs, mrt} from '@datagrok-ai/diff-studio-tools';Next, we create
const task: ODEs = {
name: 'Example', // name of your model
arg: {
name: 't', // name of the argument
start: 0, // initial value of the argument
finish: 2, // final value of the argument
step: 0.01, // solution grid step
},
initial: [1, -1], // initial values
func: (t: number, y: Float64Array, output: Float64Array) => { // right-hand side of the system
output[0] = y[0] + y[1] - t; // 1-st equation
output[1] = y[0] * y[1] + t; // 2-nd equation
},
tolerance: 1e-7, // tolerance
solutionColNames: ['x', 'y'], // names of solution functions
};Finally, we call the specified numerical method to solve task:
const solution = mrt(task);Currently, solution contains:
solution[0]- values of $t$, i.e. the range $0..2$ with the step $0.01$solution[1]- values of $x(t)$ at the points of this rangesolution[2]- values of $y(t)$ at the points of the same range
Find this example in basic-use.ts.
Performance
The following classic problems are used to evaluate efficiency of Diff Grok methods:
- Rober
- a stiff system of 3 nonlinear ODEs
- describes the kinetics of an autocatalytic reaction given by Robertson
- robertson.ts
- HIRES
- a stiff system of 8 non-linear equations
- explains the `High Irradiance Responses' (HIRES) of photomorphogenesis on the basis of phytochrome, by means of a chemical reaction involving eight reactants
- hires.ts
- VDPOL
- a system of 2 ODEs proposed by B. van der Pol
- describes the behaviour of nonlinear vacuum tube circuits
- vdpol.ts
- OREGO
- a stiff system of 3 non-linear equations
- simulates Belousov-Zhabotinskii reaction
- orego.ts
- E5
- a stiff system of 4 non-linear ODEs
- represents a chemical pyrolysis model
- e5.ts
- Pollution
- a stiff system of 20 non-linear equations
- describes a chemical reaction part of the air pollution model designed at The Dutch National Institute of Public Health and Environmental Protection
- pollution.ts
The MRT, ROS3PRw and ROS34PRw methods demonstrate the following time performance (AMD Ryzen 5 5600H 3.30 GHz CPU):
| Problem | Segment | Points | Tolerance | MRT, ms | ROS3PRw, ms | ROS34PRw, ms |
|---|---|---|---|---|---|---|
| Rober | 0, 10E+11 | 40K | 1E-7 | 103 | 446 | 285 |
| HIRES | 0, 321.8122 | 32K | 1E-10 | 222 | 362 | 215 |
| VDPOL | 0, 2000 | 20K | 1E-12 | 963 | 1576 | 760 |
| OREGO | 0, 360 | 36K | 1E-8 | 381 | 483 | 199 |
| E5 | 0, 10E+13 | 40K | 1E-6 | 14 | 17 | 8 |
| Pollution | 0, 60 | 30K | 1E-6 | 36 | 50 | 23 |
Run check-methods.ts to check results.
Scripting
The library provides tools for declarative specifying models defined by IVPs. This feature enables a development of "no-code" modeling tools seamlessly integrated with the Datagrok platform.
Model components and syntax
Each model has a simple declarative syntax.
Core blocks
These blocks define the basic mathematical model and are required for any model:
#name: Add a model identifier#name: Problem#equations: Define the system of ODEs to solve. Diff Grok supports any number of equations with single or multi-letter variable names#equations: dx/dt = x + y + exp(t) dy/dt = x - y - cos(t)#argument: Defines- independent variable
- its initial value (
initial) - final value (
final), and - grid step (
step)
The solver calculates values at each step interval across the specified initial,final range.
#argument: t initial = 0 final = 1 step = 0.01#inits: Defines initial values for functions being solved#inits: x = 2 y = 5
Comments
#comment: Write a comment in any place of your model#comment: You can provide any text here. The lib ignores it.Place comments right in formulas using
//#equations: dx/dt = x + y + exp(t) // 1-st equation dy/dt = x - y - cos(t) // 2-nd equation
Model parameters
These blocks define values used in equations. Choose type based on intended use:
#parameters: Generate UI controls for model exploration#parameters: P1 = 1 P2 = -1#constants: Use for fixed values in equations that don't require UI controls#constants: C1 = 1 C2 = 3
Auxiliary calculations
This block defines mathematical functions using #parameters, #constants,
#argument, and other functions. These are direct calculations (no ODEs involved). Use them to break
down complex calculations and simplify your equations.
#expressions#expressions: E1 = C1 * t + P1 E2 = C2 * cos(2 * t) + P2
JS-code generation
To transform any model to JavaScript code with an appropriate specification of ODEs object, follow the steps:
- Import the parsing and code generating tools:
import {getIVP, getJScode} from '@datagrok-ai/diff-studio-tools';- Define a string with a model specification, use a simple model syntax:
const model = `
#name: Example
#equations:
dx/dt = x + y - cos(t)
dy/dt = x - y + sin(t)
...
`;- Parse formulas:
const ivp = getIVP(model);The method getIVP parses formulas and returns IVP object specifying a model.
- Generate JS-code:
const lines = getJScode(ivp);The method getJScode transforms IVP object to JavaScript code. It returns an array of strings with this code.
Find this example in scripting.ts.
Pipelines
Diff Grok pipeline is a powerful feature for complex process simulation and model analysis in webworkers. It wraps the main solver with a set of actions that perform pre- and post-processing of a model inputs & outputs. In addition, they provide an output customization.
- Start with imports:
import * as DGL from '@datagrok/diff-grok';- Define your model:
const model = `#name: My model
#equations:
dx/dt = ...
dy/dt = ...
...
#inits:
x = 2
y = 3
...- Generate IVP-objects:
- for the main thread computations:
const ivp = DGL.getIVP(model);- for computations in workers:
const ivpWW = DGL.getIvp2WebWorker(ivp);- Set model inputs:
const inputs = {
x: 2,
y: 30,
...
};- Create typed input array:
const inputVector = DGL.getInputVector(inputs, ivp);- Get a pipeline:
const creator = DGL.getPipelineCreator(ivp);
const pipeline = creator.getPipeline(inputVector);You can pass pipeline, ivpWW, and inputVector to webworkers.
- Apply pipeline to perform computations:
const solution = DGL.applyPipeline(pipeline, ivpWW, inputVector);Find complete examples in these files:
- pipeline-use.ts - A basic example demonstrating pipeline usage
- model-updates.ts - A simulation of a multi-stage process using pipelines
- cyclic-model.ts - A simulation of a cyclic process using pipelines
Integration with Datagrok
Datagrok is a platform enabling powerful scientific computing capabilities. It provides next-generation environment for leveraging interactive visualizations, data access, machine learning, and enterprise features to enable developing, publishing, discovering, and using scientific applications.
The library is seamlessly integrated to Datagrok via the Diff Studio package. It provides
- Numerical solving IVPs directly in the browser
- "No-code" models development
- Solving both stiff and non-stiff systems of ODEs
- Automatic generation of user interfaces
- Interactive visualization and model exploration
- Sensitivity analysis and parameters optimization
- Sharing models and computational results
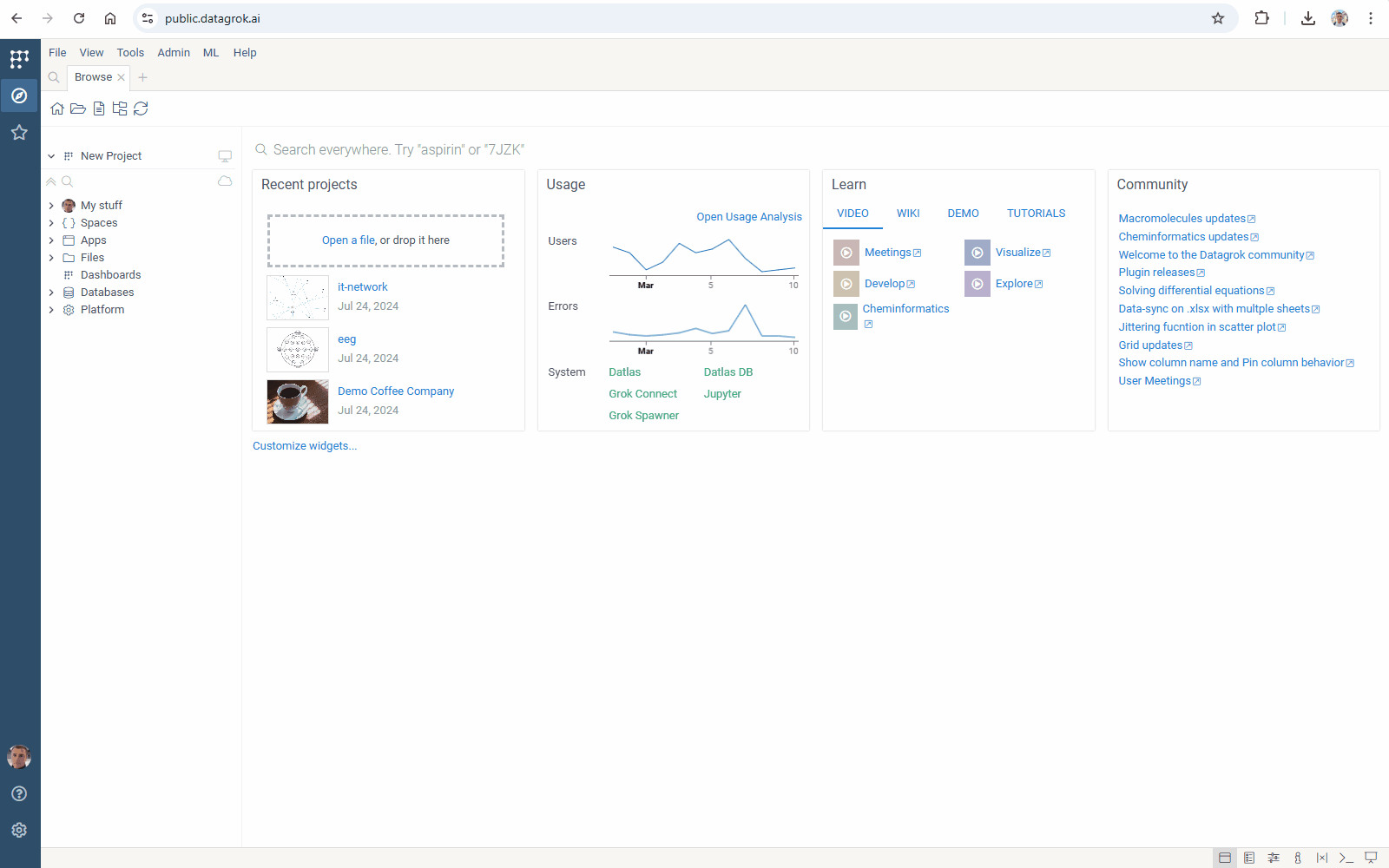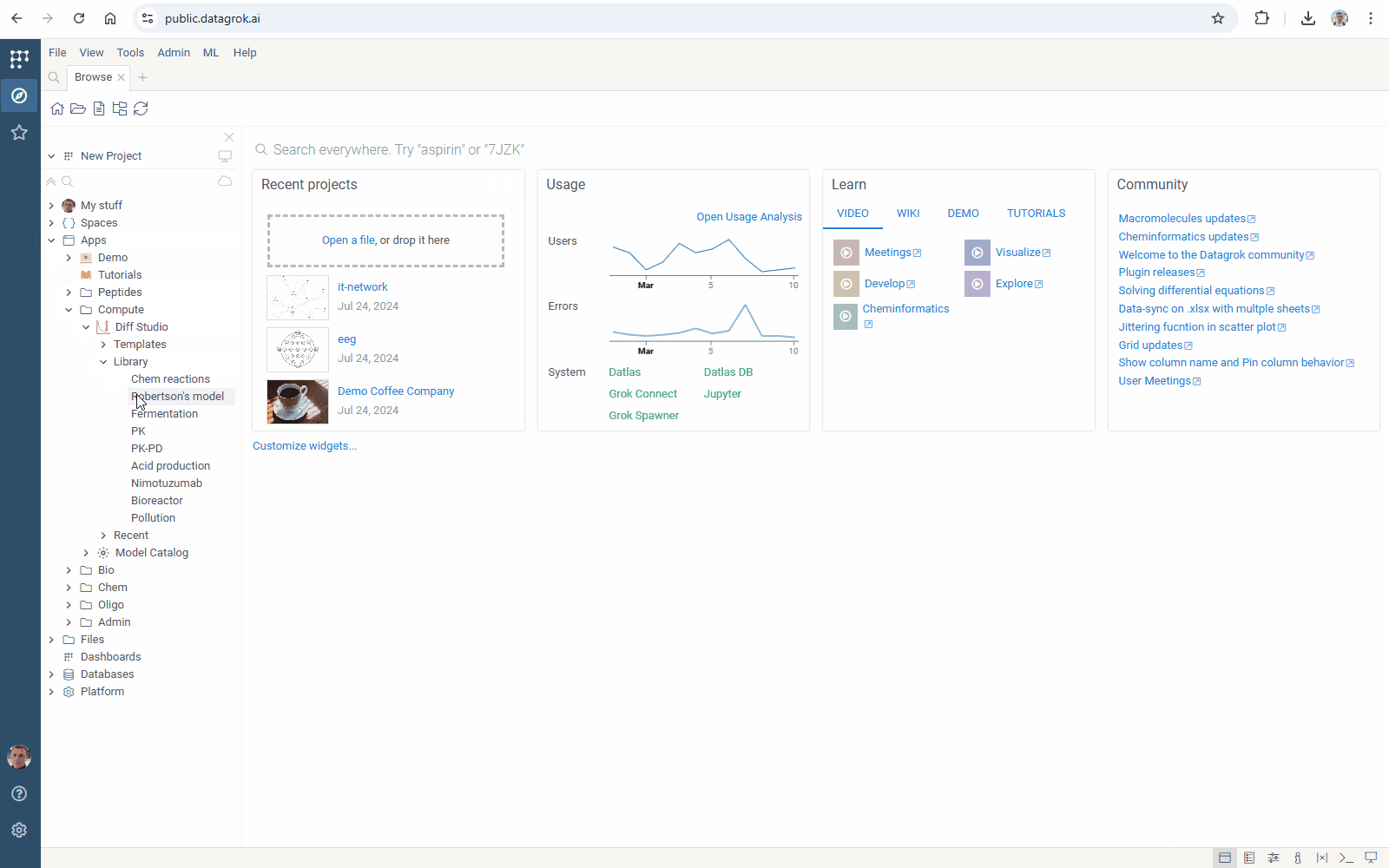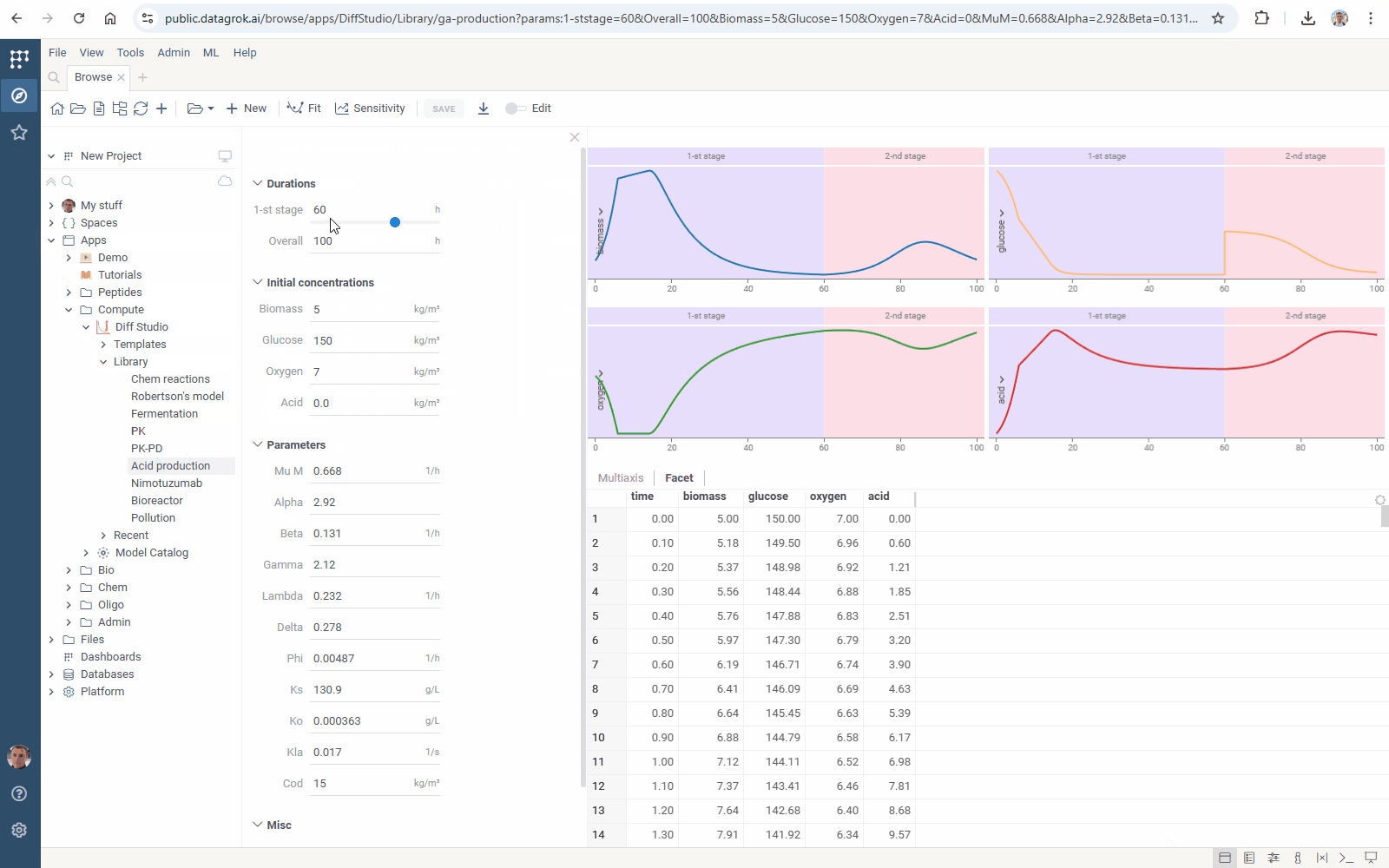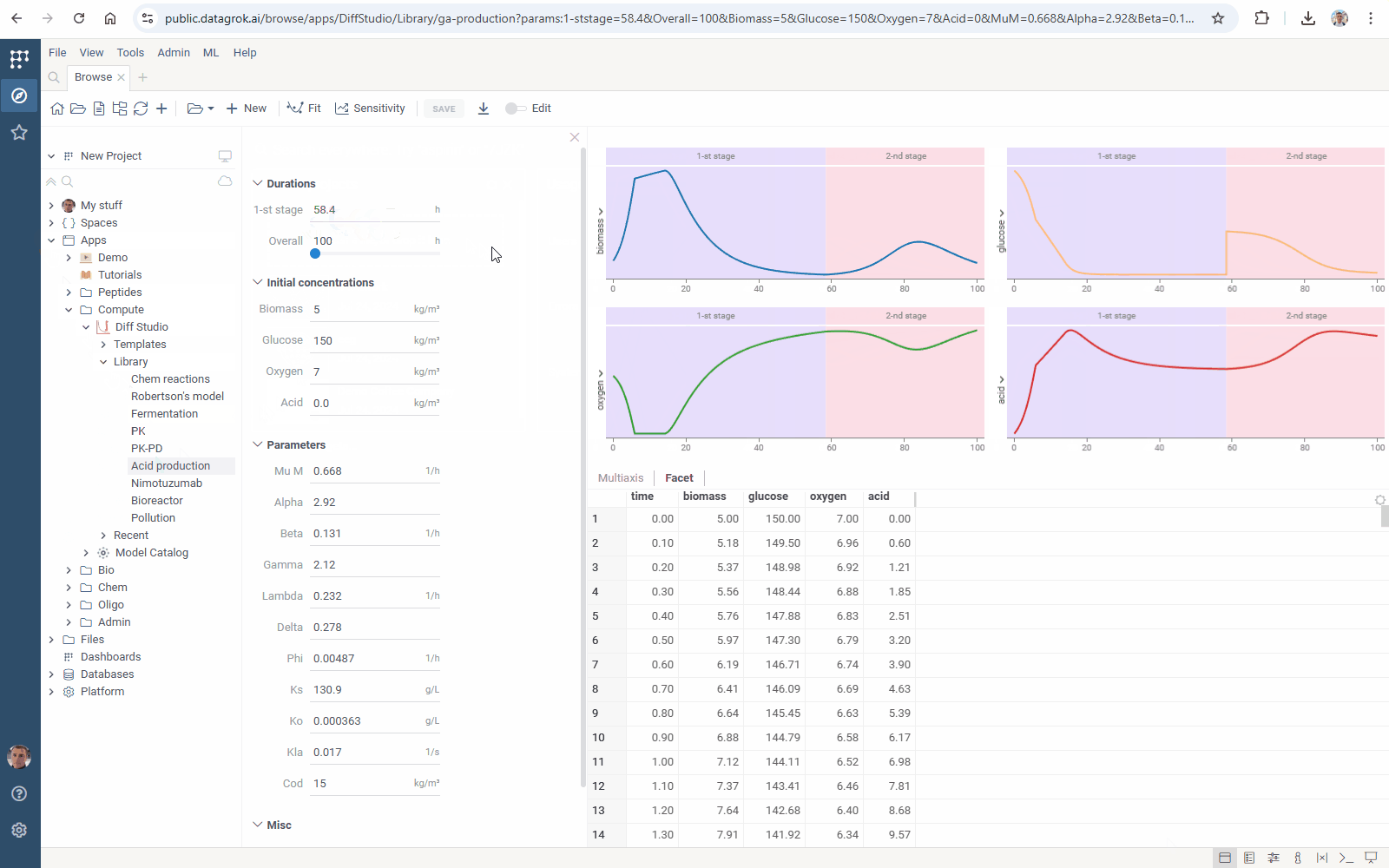
Run the Diff Studio app and check interactive modeling:
Learn more
- Diff Studio application docs
- Diff Studio example models
- Parameters optimization
- Sensitivity analysis