warp-grid v2.4.4

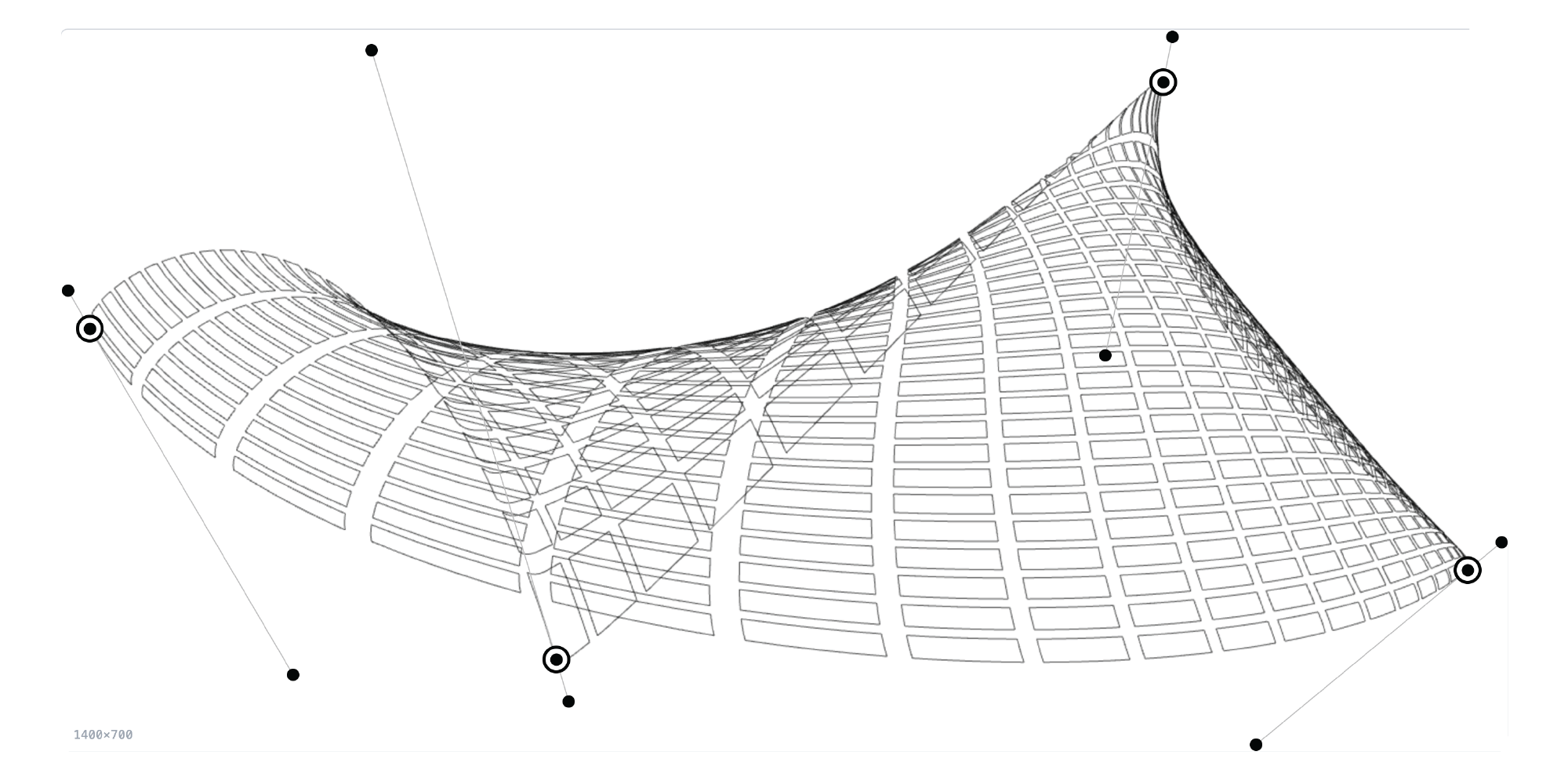
This package allows you to create a complex grid and distort it, taking the concept of a Coons patch and applying it to a grid system, meaning the grid is not bounded by four straight lines, but by four cubic Bézier curves. This allows you to create some very strange an interesting grids that would be very difficult to generate with traditional graphics software.

There is an editor which allows you to generate and manipulate a grid, giving access to all the configuration available.

The package provides a set of powerful configuration options to define the grid including variable width columns and gutters, control over distribution of rows and column distribution using Bézier easing, and access to different types of interpolation, as well as the option to provide your own interpolation.

Its API gives you access to information about the grid's metrics: its bounds, rows, columns, gutters and cells. It is designed so that the metrics for an individual grid-cell can be used as bounds for another grid, allowing nested grids.

This package does not handle any rendering itself, but provides you with all the data you need to render the grid using SVG, Canvas or anything else you like.

If you just want to generate a coons-patch, you can use an underlying package called coons-patch.

Install package

pnpm add warp-grid
# or
npm add warp-grid
# or
yarn add warp-grid

Package Documentation (TSDoc generated).

This package is written in TypeScript and exports its types.

Quick-start

The basic workflow is that you supply bounds representing the edges of your grid, and a grid configuration object describing the grid you'd like to map onto the bounds. You receive an object with information about the grid, and an API to allow you to get information about the grid. This means no expensive calculations are done up front, and calculations are only performed when you need them.

import warpGrid from 'warp-grid'

// Define bounding (cubic Bézier) curves for the patch
const boundingCurves = {
  top: {
    startPoint: { x: 0, y: 0 },
    endPoint: { x: 100, y: 0 },
    controlPoint1: { x: 10, y: -10 },
    controlPoint2: { x: 90, y: -10 },
  },
  bottom: {
    startPoint: { x: 0, y: 100 },
    endPoint: { x: 100, y: 100 },
    controlPoint1: { x: -10, y: 110 },
    controlPoint2: { x: 110, y: 110 },
  },
  left: {
    startPoint: { x: 0, y: 0 },
    endPoint: { x: 0, y: 100 },
    controlPoint1: { x: -10, y: -10 },
    controlPoint2: { x: -10, y: 110 },
  },
  right: {
    startPoint: { x: 100, y: 0 },
    endPoint: { x: 100, y: 100 },
    controlPoint1: { x: 110, y: -10 },
    controlPoint2: { x: 110, y: 110 },
  },
}

// Define a 10 x 5 grid with gutters
const gridDefinition = {
  columns: 10
  rows: 5,
  gutters: 2
}

const grid = warpGrid(
  boundingCurves,
  gridDefinition
)

// Get a point on the patch at the provided horizontal and vertical ratios (0–1 inclusive)
const point = warpGrid.getPoint(0.5, 0.75)

// Get an Array containing all the curves along the x-axis.
const curvesXAxis = warpGrid.getLinesXAxis()

// Get an Array containing all the curves along the y-axis.
const curvesXAxis = warpGrid.getLinesYAxis()

// Get an Array containing all the curves along the both the x- and y-axis.
const curves = warpGrid.getLines()

// Get an array of points representing every point on the grid where lines intersect.
const intersections = warpGrid.getIntersections()

// Get the bounds for the grid-square at the supplied coordinates
const bounds = warpGrid.getCellBounds(3, 8)

// Get an array containing the bounds for every grid-square
const allBounds = getAllCellBounds()

Usage

Primitives

There are a number of data types that are used by the package to describe aspects of the grid:

Points look like this:

const point = {
  x: 34,
  y: 44
}

All curves are represented by cubic Bézier curves:

const curve = {
  startPoint: {
    x: 0,
    y: 0
  },
  controlPoint1: {
    x: 0,
    y: 33
  },
  controlPoint2: {
    x: 0,
    y: 66
  },
  endPoint: {
    x: 0,
    y: 100
  }
}

Bounding curves look like this, where each item is curve.

const boundingCurves = {
  top: { … },
  bottom: { … },
  left: { … },
  right: { … }
}

Bounding curves

To generate a grid you must provide a set of four bounding curves (top, left, bottom and right) in the form of four cubic Bézier curves. A cubic Bézier curve describes a straight-line or curve using a start point (startPoint), an end point (endPoint) and two other control points(controlPoint1 and controlPoint2). Each point has an x and y coordinate.

At minimum you must supply start and end points for each curve. If you do not supply controlPoint1 it will be set to the same coordinates as the start point, and if you do not supply controlPoint2 it will be set to the same coordinates as the end point. Setting both control points to the same values as the start and end point will result in a straight line. You also need to ensure that the four curves meet at the corners.

You will probably be expecting the end of each curve to be the start of the next, however in keeping with the math involved in generating a coons-patch this is not the case. The top and bottom curves run left to right, and left and right curves run top to bottom, so this means that:

• the startPoint of the top curve must share the same coordinates with the startPoint of the left curve.
• the endPoint of the top curve must share the same coordinates with the startPoint of the right curve.
• the startPoint of the bottom curve must share the same coordinates with the end point of the left curve.
• the endPoint of the bottom curve must share the same coordinates with the endPoint of the right curve.

         top
      -------->
left |         | right
     ↓ ------> ↓
       bottom

Note that when you are getting cell bounds back from the API, both getCellBounds and getAllCellBounds accept a config object which has a makeBoundsCurvesSequential key. If this is set to true, the order of the bounding curves is made sequential:

         top
     ↑ ------->
left |         | right
      <------- ↓
       bottom

Grid definition

The grid definition is an object describing the grid you are modelling. It will be merged with a set of defaults.

Columns and Rows

columns and rows define the number of columns and rows in the grid. A grid has a minimum of one row and one column. The generic name for columns and rows used in the following docs is steps.

These fields can be one of the following:

1. An integer, in which case that integer will represent the number of columns or rows. For example columns: 2, will result in a grid with two columns.

2. An array of integers, in which case the number of steps will equal the number of items in the array, with the size of each step consisting of the value of that array item as an integer of the total of all the values. For example, columns: [3, 5, 1, 1] will result in a total of 10 (3 + 5 + 1 + 1), meaning that the first column will be 3/10 (30%) of the grid width, the second column 5/10 (50%), and the remaining two columns 1/10 (10%) each.

3. An array of objects, each with a value key: ({ value: 2}). This will work the same as the previous example, with the combined value of all the value keys dictating the total value, and the value key dictating the size of each step.

{
  columns: [
    2,
    3,
    1
  ],
  rows: [
    1,
    1,
    1,
    5,
    5
  ],
  …
}

It is also possible to add gutters here (see below).

Gutters

gutter describes the width of horizontal gutters and the height of vertical gutters. Gutters are the spaces between the grid cells. If gutter is a number, it describes both horizontal and vertical gutters. If it is an array of two numbers, the first number describes the horizontal gutter and the second number describes the vertical gutter. Like columns and rows, gutters are also a ratio of the total value, for example, if columns are [1,4,3] and gutters are 1 then the total will be 10 (1 + 4 + 3 + (2 * 1)). There will be three rows of 1/10 (10%), 4/10 (40%) and 3/10 (30%) with two gutters of 1/10 (10%) between them.

There is an additional way to add gutters without using the gutters property. You can add them to the rows or columns arrays, using an object with a value property, but also adding an isGutter property set to true: ({ value: 2. isGutter: true}). This allows you to define gutters of different widths/heights in the same way you can define columns or rows of different widths/heights.

{
  gutter: [
    2,
    3
  ],
  …
}

### Interpolations

A lot of the work done by the package involves interpolation. The grid also supports configuration params that change how it performs these interpolations.

interpolationStrategy

interpolationStrategy changes the algorithm used to interpolate the position of points along a curve. These algorithms are used in calculating the location of points within the bounds. This value can be either a string, a function, or a tuple of two functions.

If it's a string it can be either even (the default) or linear. linear is a simple form of interpolation that results in a distribution that is affected by the amount of curvature of the bounds. even uses a more complex approach and usually results in more evenly distributed results. However this comes at the cost of performance.

Alternatively a single factory function, or a tuple of two factory functions (one for each axis) can be supplied.

{
  lineStrategy: `even`,
  …
}

These functions comprise of a factory function that accepts a configuration object and returns an interpolation function. The factory function is called internally using config from the grid definition object.

Factory functions for both linear and even interpolation are exported by this package:

• interpolatePointOnCurveEvenlySpacedFactory
• interpolatePointOnCurveLinearFactory

If you use your own interpolation factory function it should have the following signature.

(config: {precision: number, bezierEasing: BézierEasing}) => (t: number, curve: Curve): Point

##### Factory

• config is an object with a precision key that can be used to control the precision of interpolation, and bezierEasing which is an object with bezierEasing values for modifying distribution for each axis. If your interpolation function doesn't require any configuration you can just use an empty function.

Interpolation function

• t is the ratio along the axis (0–1 inclusive).
• curve is a cubic Bézier curve along which the interpolation will be used.

lineStrategy

lineStrategy controls how the grid lines are interpolated and can either be straightLines or curves. The lines returned from getCurves, getCurvesXAxis and getCurvesYAxis, and the bounds returned from getCellBounds and getAllCellBounds are always represented by cubic Bézier curves, however if the lineStrategy is straightLines (the default), the calculations are significantly simplified and all lines will be straight (controlPoint1 will be the same as the startPoint, and controlPoint2 will be the same as endPoint) For more accurate calculations choose curves which will draw curved cubic Bézier curves at the expense of performance.

{
  lineStrategy: `curves`,
  …
}

precision

If you choose to use a line strategy of even, this parameter controls how precise the interpolation is. Higher values are more memory-intensive but more accurate. The default value is 20. With linear this will have no effect.

{
  precision: 5
  …
}

bezierEasing

The grid provides a very powerful way of controlling the distribution of lines along each access using bezierEasing. Bézier easing is widely used for animation as a way of providing easing to a changing value. Instead of applying easing to an animation, here it is applied to the interpolation of points along an axis. bezierEasing is implemented internally by first creating an easing function, and then passing a value (in the range of 0–1) to it. The easing function requires four values (each from 0–1). The first two values represent the position of the first control point (x, y) and the last two values represent the position of the second control point. So the value for bezierEasing will look like this:

{
  bezierEasing: {
    u: [0, 0, 1, 1]
    v: [0, 0, 1, 1]
  }
  …
}

The easiest way to understand what effect the different values have is to play with the editor.

Here is a full example of a grid definition:

{
  columns: 8,
  rows: [10, 5, 20, 5, 10],
  gutters: [5, 3],
  interpolationStrategy: `even`,
  lineStrategy: 'curves',
  precision: 30,
  bezierEasing: {
    u: [0, 0.5, 1, 1]
    v: [0, 0, 0.3, 1]
  }
}

Return value

The return value is a warp grid object representing the grid and providing an API to interrogate it.

{
  model: {
    columns,
    rows,
    boundingCurves
  },
  getPoint,
  getLinesXAxis,
  getLinesYAxis,
  getLines,
  getIntersections,
  getCurves,
  getCellBounds,
  getAllCellBounds,
}

Model object

model provides access to the resolved configuration data that was used to generate the patch. The configuration data is not the same as the data you passed in, but is instead the internal representation of that data.

• columns contains an array of column values. This will always be made up of objects, regardless of how you supplied them.
• rows contains an array of row values. This will always be made up of objects, regardless of how you supplied them.
• boundingCurves contains the bounding curves object that was passed in.

API

Important note

One of the powerful features of this package is that a grid cell can itself be used as bounds for another grid. To achieve this, the bounding curves returned from getCellBounds and getAllCellBounds follow the same pattern as the bounding curves used to define the grid, meaning the top and bottom curves run left-to-right and the left and right curves run top-to-bottom.

• getPoint(x, y) returns the point on the grid at the supplied x and y ratios.Both x and y should be a number from 0–1 inclusive. For example, an x of 0 and a y of 0 would return a point in the top left corner. An x of 1and a y of 1 would return a point the top right corner.

• getLinesXAxis() returns an array representing all the curves for each step along the x-axis. This includes curves for all left and right edges.

• getLinesYAxis() returns an array representing all the curves for each step along the y-axis. This includes curves for all top and bottom edges.

• getLines() returns an object with xAxis and yAxis keys, each of which contains an array representing all the curves for each step along that axis.

• getIntersections() returns an array of points, one for every point at which an x-axis line intersects with a y-axis line.

• getCellBounds(row, column) returns a set of bounding curves for the cell at the supplied row and column. Row and column are zero-based.

• getAllCellBounds() returns an array of bounding curves for all the cells in the grid.

Dependencies

This project has four dependencies:

• coons-patch to calculate points on a surface defined by Bézier curves.
• fast-memoize for memoization.
• bezier-easing for creating Bézier-easing functions.
• matrix-js for matrix math

## Thanks

Thanks to pomax for his help (and code) for curve fitting (which is much more complex than it might seem). His A Primer on Bézier Curves is a thing of wonder.

Maintenance

Install

pnpm install

Build

pnpm run build # Build once
pnpm run build-watch # Build and watch for changes

Preview build

pnpm run preview

Generate docs

pnpm run docs

View the generated docs

pnpm run docs-view

Run unit tests

Unit tests use vitest.

pnpm run test # Run tests once
pnpm run test-watch # Run tests and watch for changes
pnpm run test-coverage # Run tests and output a coverage report
pnpm run test-snapshot # Regenerate snapshots

Lint

pnpm run lint-prettier
pnpm run lint-eslint

Linking

To link into the local version of coons-patch for local testing run:

pnpm run link

To unlink (and install the package from npm):

pnpm run unlink

Release

Releases are via semantic-release and executed on CI via Github actions.

The following steps are run as part of the actions pipeline

• Code is linted
• Unit tests are run
• TypeScript is compiled to JavaScript
• Package is released (if previous stages all pass)